本文主要描述了图像之间的各种变换：平移；翻转；翻转+平移；相似变换；仿射；投影
##2D图像变换
- 平移：
2维平面的平移可以写成：\(x' = x + t\)或者\(x' = [I\ t] \bar x\),其中\(I\)是\(（2*2）\) 的单位矩阵,\(\bar x=(x,y,1)\)是平面坐标。 - 翻转+平移（刚体运动或者欧几里德变换）：
\(\bar x = Rx+t\)或者是\(\bar x = [R\ t]x\),其中 \(R=[\begin{matrix} \cos \theta & -\sin \theta \cr \sin \theta & cos \theta \end{matrix}]\) 是标准正交旋转矩阵\(RR^T=I,|R|=1\) - 相似变换：是仿射变换的一种
\(x'=sRx+t\)其中\(s\)是任意尺度因子，也可以写成 \(x'=[sR \ \ t]x= [\begin{matrix} a & -b & t_x\cr b & a & t_y\cr \end{matrix}]x\) 其中我们没必要要求\(a^2+b^2=1\),其实他相当于两条直线转换。 - 仿射变换：
\(x'=Ax\),其中\(A\)是一个2*3的矩阵，或者可以写成： \(x'=[\begin{matrix} a_{00} & a_{01} & a_{02} \cr a_{10} & a_{11} & a_{12} \end{matrix}]x\) 在仿射变幻中平行线仍保持平行。 - 透视变换（单应性）：
\(x' ~ Hx\),其中\(x',x\)是在齐次坐标暂时可以理解成矩阵\(x'=(x,y),x=(x,y,1)\)；\(H\)是一个任意的\(3*3\)的矩阵，且是齐次的；\(~\)表示的是一种运算符，可以通过下式来理解： \(x'= {h_{00}x+h_{01}y+h_{02} \above 1pt h_{20}x+h_{21}y+h_{22}}\), \(y'= {h_{10}x+h_{11}y+h_{12} \above 1pt h_{20}x+h_{21}y+h_{22}}\). 在经过透视变换后直线还是直线。但是平行线就不一定平行了。 也可以参照该网站理解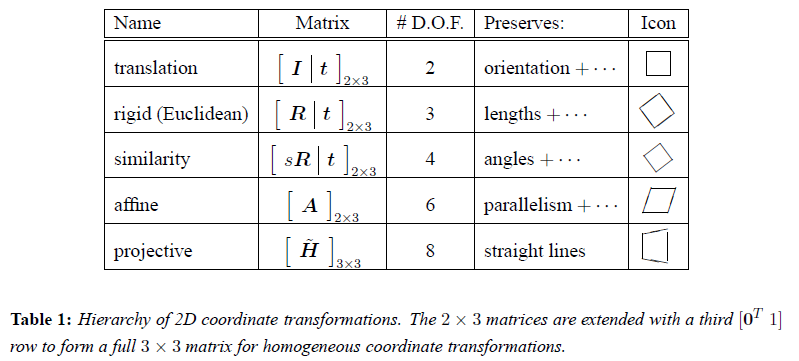
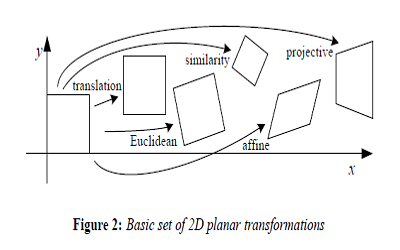1-5变换都是在2D图像上的，的在上边两个图形象表示。上边内容参考的是Image Alignment and Stitching:A Tutorial1 的2.2节。
##接下来介绍3D变换## 相应的上边1-5变换在3D中同样应用，但是矩阵要变换成\(4*4\)。
Click the link below to go back to index:
Go back