本文主要讲解各种插值方法：1，最近邻插值；2，双线性插值；3，双三次插值
- 最近邻插值：
这是最简单的一种插值方法，不需要计算，在待求象素的四邻象素中，将距离待求象素最近的邻象素灰度赋给待求象素。设i+u, j+v(i, j为正整数， u, v为大于零小于1的小数，下同)为待求象素坐标，则待求象素灰度的值 f(i+u, j+v) 如下图所示：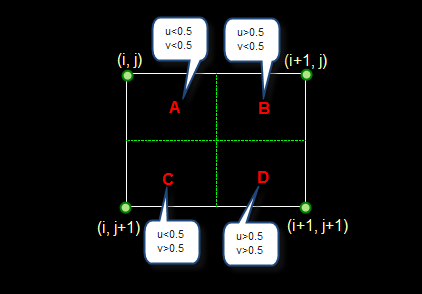
如果(i+u, j+v)落在A区，即u<0.5, v<0.5，则将左上角象素的灰度值赋给待求象素，同理，落在B区则赋予右上角的象素灰度值，落在C区则赋予左下角象素的灰度值，落在D区则赋予右下角象素的灰度值。
最邻近元法计算量较小，但可能会造成插值生成的图像灰度上的不连续，在灰度变化的地方可能出现明显的锯齿状。 - 双线性插值:
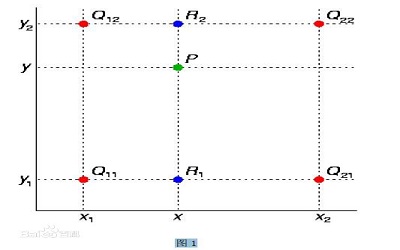
已知的红色数据点与待插值得到的绿色点
假如我们想得到未知函数f在点P= (x,y) 的值，假设我们已知函数f在Q11 = (x1,y1)、Q12 = (x1,y2),Q21 = (x2,y1) 以及Q22 = (x2,y2) 四个点的值。
首先在x方向进行线性插值，得到R1和R2，然后在y方向进行线性插值，得到P。这样就得到所要的结果f(x,y).其中红色点Q11,Q12,Q21,Q22为已知的4个像素点.
公式可以表示为：\(f(\bar x,\bar y) = (1-a)(1-b)f(x,y) + a(1-b)f(x+1,y) +(1-a)bf(x,y+1) + abf(x+1,y+1)\),其中\(a = \bar x -x, b = \bar y - y，y为\bar y的取整\) 双线性插值的一个显然的三维空间延伸是三线性插值。当对相邻四个像素点采用双线性插值时，所得表面在邻域处是吻合的，但斜率不吻合。并且双线性灰度插值的平滑作用可能使得图像的细节产生退化，这种现象在进行图像放大时尤其明显。 - 双三次插值(自己认为也是单样条插值):
双三次插值是一种更加复杂的插值方式，它能创造出比双线性插值更平滑的图像边缘。双三次插值通常能产生效果最好，最精确的插补图形，但它速度也几乎是最慢的。“双线性插值”（Bilinear interpolation）的速度则要快一些，但没有前者精确。
该方法利用三次多项式S(x)求逼近理论上最佳插值函数sin(x)/x, 其数学表达式为： \(s(x)=\lbrace{\begin{matrix} 1-2|x|^2+|x|^3 & 0 \leqslant |x| < 1 \cr 4-8|x|+5|x|^2-|x|^3 & 1 \leqslant|x|<2 \cr 0 & |x| \geqslant 2 \end{matrix}}\) 待求像素(x, y)的灰度值由其周围16个灰度值加权内插得到，如下图：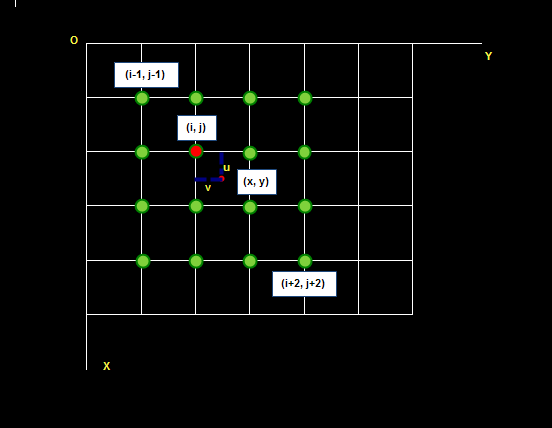
待求像素的灰度计算式如下：\(f(x, y) = f(i+u, j+v) = ABC\) 其中：\(A={\left\lgroup \matrix{s(1+v) \cr s(v) \cr s(1-v) \cr s(2-v)} \right\rgroup}\), \(B={\left\lgroup \matrix{f(i-1,j-1) & f(i-1,j) & f(i-1,j+1) & f(i-1,j+2) \cr f(i,j-1) & f(i,j) & f(i,j+1) & f(i,j+2) \cr f(i+1,j-1) & f(i+1,j) & f(i+1,j+1) & f(i+1,j+2) \cr f(i-2,j-1) & f(i-2,j) & f(i-2,j+1) & f(i-2,j+2)} \right\rgroup}\), \(C={\left\lgroup \matrix{s(1+u) \cr s(u) \cr s(1-u) \cr s(2-u)} \right\rgroup}\)
##Opencv函数void cvResize( const CvArr* src, CvArr* dst, int interpolation=CV_INTER_LINEAR )可实现上述三种方法，其中interpolation 修改、插补的方法，取值如下： ·CV_INTER_NN - 最近-邻居插补 ·CV_INTER_LINEAR - 双线性插值（默认方法） ·CV_INTER_AREA - 像素面积相关重采样。当缩小图像时，该方法可以避免波纹的出现。当放大图像时，类似于方法CV_INTER_NN。（It is the preferred method for image decimation that gives moire-free results. In case of zooming it is similar to CV_INTER_NN method. ） ·CV_INTER_CUBIC - 双三次插值。
Click the link below to go back to index:
Go back