本文主要讲述了最基本的几个关于导数和二阶导数的矩阵如:梯度,Jacobi 矩阵,拉普拉斯矩阵,Hesse 矩阵。
- 梯度(一阶导数)
对于一个含有 n 个变量的标量函数,即函数输入一个 n 维 的向量,输出一个数值,梯度可以定义为:
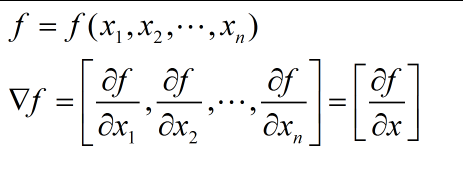
- Jacobi 矩阵
Jacobi 矩阵实际上是向量值函数的梯度矩阵,假设F:Rn→Rm 是一个从n维欧氏空间转换到m维欧氏空间的函数。这个函数由m个实函数组成 。这些函数的偏导数(如果存在)可以组成一个m行n列的矩阵(m by n),这就是所谓的雅可比矩阵:
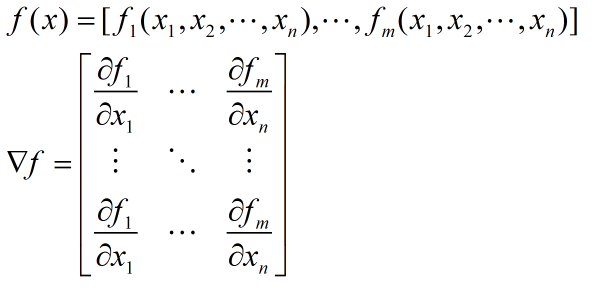
- 拉普拉斯矩阵
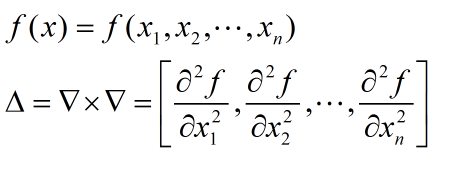
其中就常用的就是高斯拉普拉斯算子:可参考这里The Laplace Operator(注意零交点)和Laplacian of Gaussian (LoG),其实就是对高斯函数的对X,Y的二阶导数和。高斯差分矩阵 - Hesse 矩阵(二阶导数)
Hesse 矩阵常被应用于牛顿法解决的大规模优化问题,主要形式如下:
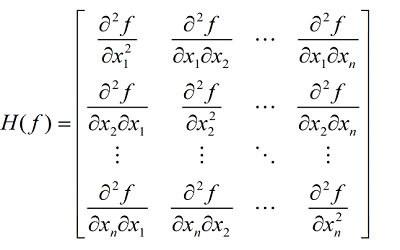
当 f(x) 为二次函数时,梯度以及 Hesse 矩阵很容易求得。二次函数可以写成下列形式:\(f(x)=1/2x^TAx+b^Tx+c\),其中 A 是 n 阶对称矩阵,b 是 n 维列向量, c 是常数。\(f(x)\) 梯度是 \(Ax+b\), Hesse 矩阵等于 A。
a) 如果 f(x) 是一个标量函数,那么雅克比矩阵是一个向量,等于 f(x) 的梯度, Hesse 矩阵是一个二维矩阵。如果 f(x) 是一个向量值函数,那么Jacobi 矩阵是一个二维矩阵,Hesse 矩阵是一个三维矩阵。
b) 梯度是 Jacobian 矩阵的特例,梯度的 jacobian 矩阵就是 Hesse 矩阵(一阶偏导与二阶偏导的关系)。
参考网址:机器学习中导数最优化方法(基础篇)
Click the link below to go back to index:
Go back